クロームブックでわさびの授業

「指導教諭から学び隊」という授業公開が10月27日に明道小で行われます。

そこで公開される、6年担任先生の「子どもが主役」「わさびの授業」を皆さん楽しみにしておられます。

 

さて。

授業クラス、5年生で行われます。

さあ。

公開2日前。5年生は、どんな授業をしているのかな？

 

異例の

公開授業前の

オンライン授業公開です。

まずは。

前時までのまとめ。

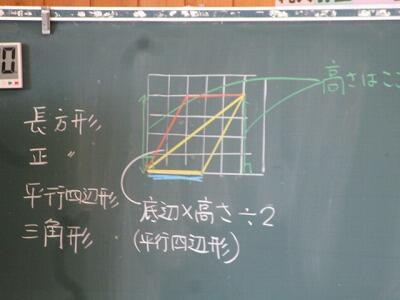
面積の公式は。

長方形や正方形、平行四辺形や三角形に形を変えて求める。

工夫すると、公式になっていく。

では。

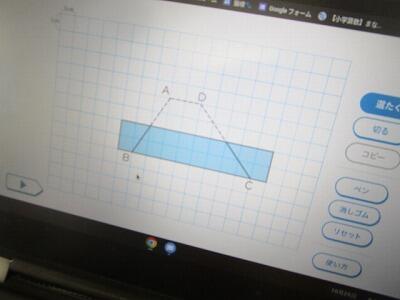
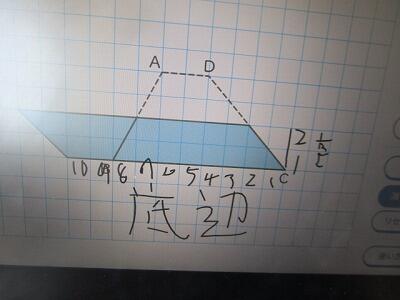
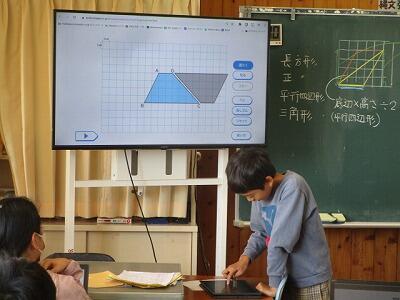
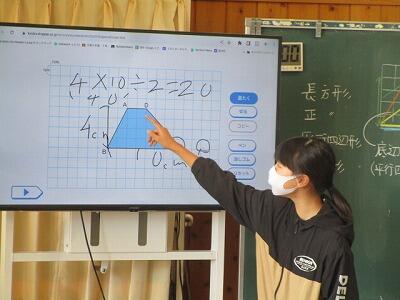
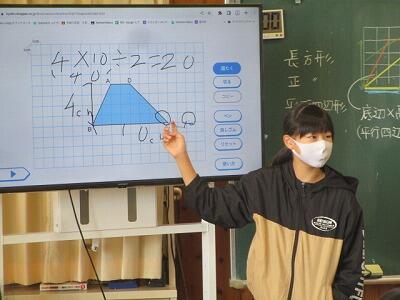
台形の面積の公式を求めてみよう！

 

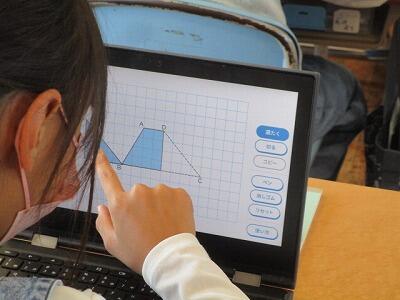
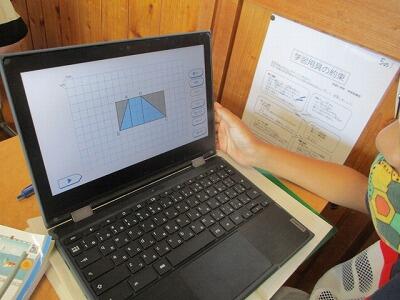
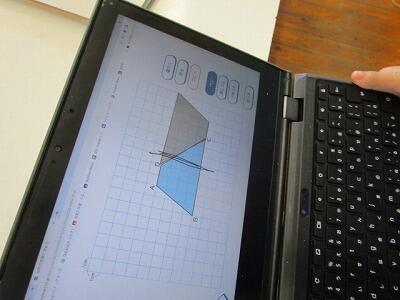
今日は、クロームブックで台形の公式を求めていきます。

みんないろんな考えをしていますよ。

ノートと違って。

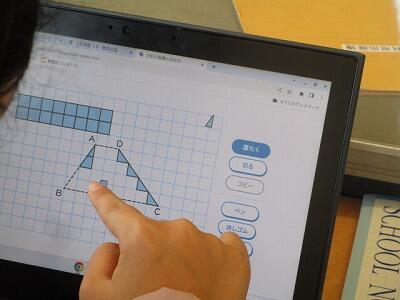
形を切ったり、貼ったり、簡単に操作できます。

みんなどうにか、三角形にしたり。

長方形にしたり。

工夫してます。

そして、苦しんでます。

なにかしら、いい感じ。

面積は、求められるようです。

なるほど。

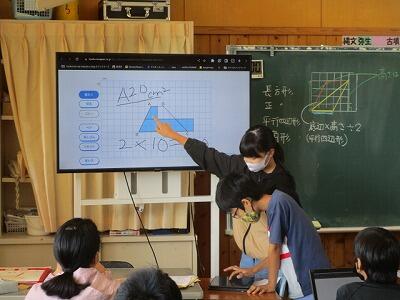
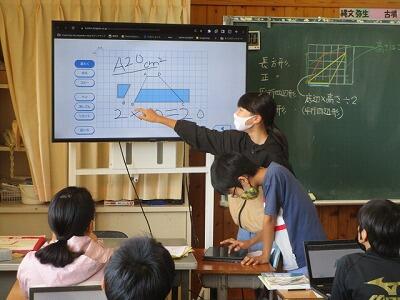
クロームブックで操作をすると、みんなの作業が一覧できるので。

子どもさんの「微細な変化に気づく」ことが容易にできます。

 

担任、終始、にこやかに「後ろから脇役に徹し」画面を眺めています。

しかし、

微細な変化が生じた子どもさんがいたら、

さっとそこに近づき、深く画面を眺めます。

 

さて。

皆、悩んでます。

そろそろ、一人の思考は限界を迎えつつあります。

・・・友達と話し合っていいですよ。

一気にクラスが動き出します。

こうだよね。

ああだよね。

回答が得られる考え方が広がっていきます。

どの考え方も、面積は求められるようです。

どの子も、この時点では、「切って三角形や四角形にする」ことにこだわっていました。

6年担任先生から指名を受けた、

ある子どもさん、スターステージに登壇。

こうすると。

三角形と四角形になりますよね。

全員の視線が熱く集まります。

教師は遥か彼方から見守ります。

教師は脇役、子どもが主役！

さあ。

回答はこの方法で求められました。

面積は２０平方センチメートル。

 

他に方法はないか、今の方法も参考にして、考えてみましょう。

「切る」にこだわる子どもたち。

こんな切り方も登場。

公式化に挑む子供も登場。

さあ。微細な変化に目を付けた、先生、次の子どもさんを指名。

 

この部分を切って。

こう動かして。

くっつける。

残りの部分を。

こう動かして。

こうすると。

長方形になるので、２×１０＝２０㎠になります。

みんなから、発表者に拍手が贈られます。

担任は、にこにこして、遠くから見つめています。

これで解決か・・・というムードが流れた時。

担任は、ある子どもさんのささやき声に反応しました。

今のささやき、

みんなに言って

みてください。

いろんな解き方が出てきて、いいと思うのですが。

どれも、「公式」にはなっていません!

ぼくたちは、「公式」を見つけなくてはいけないのです。

回答に近づいた喜びに満ちていた学級が静まり返りました。

担任は、学習が、このように流れていくと。

ちゃんと、「先を読んで」授業を構築しているのです。

そこで。

担任先生、ちょこんと板書。

子どもへの挑戦状を投げました。

子ども達から「猛」クレーム。

「先生。もう一度チャンスをください！」

「絶対、公式あるはずです。」

「もう少しなんです！」

そうですか。では。

切るだけじゃない方法も含めて、もう一度、トライしてみよう！

がぜん、子ども達のやる気が出てきました。

「教えられるだけ」の授業をこばむ子どもたちの挑戦。

自分で求めることこそが、「楽しい学び」なのだと気づいた子どもたちのこだわり。

みんなで、協働して学び取ることの楽しさを知った子どもたち。

最後まであきらめません。

絶対に自分たちで解いてやろうとする子どもが主役の授業。

先生、後ろから変わらず、にこにこと子ども達を見つめています。

しかし、いつもと違うのは・・・。

ノートでの協議ではなく。

クロームブックでの協議であるという事。

つまり、

先生の位置から、

ほぼすべての子ども達の画面は、

見えている。

ということ。

先生、ある子どもさんの画面の「微細な変化」をとらえました。

これです。

先生の御指名。「これ、発表してください。」

・・・さあ、ホームランバッター、バッターボックスに向かう！

全員の視線が、その子どもさんに集まる。

残り時間、5分。

さあ、先を読んだ教師が勝つのか。

校長、息をつめて見守ります。

子どもさん説明を始めます。

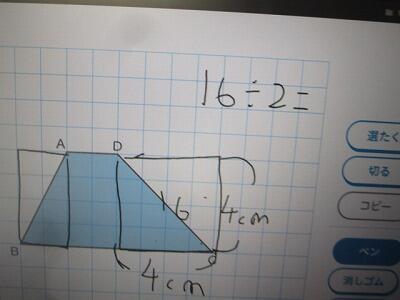
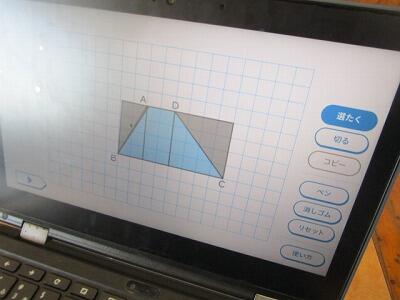
切るんじゃないんです。

コピーするんです。

え！？？

ひっつけて。

回してくっつけると。

平行四辺形になって。

底辺×高さで、面積が求められます。

大きな拍手が起きました。

でも・・・公式にはまだ届かない。

そこで、サポーターが立ち上がります。

助けます！

ここは。

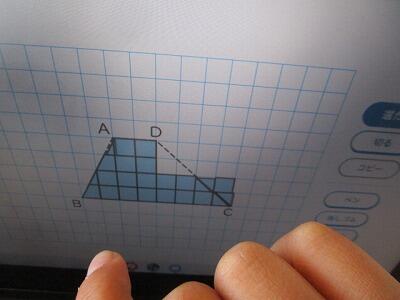
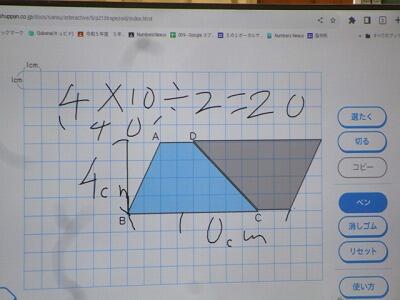
8センチで、底辺です。

問題は、ここです。

さっきまで、上の辺だった辺の２センチを足すと10センチ。

だから、４×１０÷２で、２０㎠です！

次から次にアタッカーが出てきて、公式をまとめようとしますが。

最終的に、ことばにつまります。

まだ、まだ、子どもさん、あきらめません。

挑み続けます。

１０は、台形の底辺と、この上の辺を足した長さですよね。

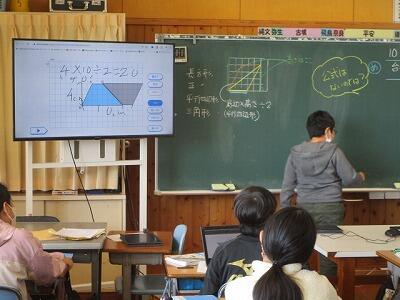
わたしが、まとめます。

ラストバッター登場。

だから、公式は。

底辺と、上の辺を足して、高さをかけて、２で割ればいいと思います。

・・・ほ、ほぼ、完成に近づきました。

 

ここで、ある子が、小さい声でつぶやきました。 

・・・底辺と「じょう（上）辺」を足すってことですよね。

でも、そのつぶやきと同時に、チャイムがなりました。

このささやきを聞いたのは、校長だけでした。

（上辺という言葉を生み出したことが、すごいと思いました。）

なるほど。

底辺に、台形の上の辺の長さを足して、平行四辺形にして、２で割ると面積が求められるのね。

 

ここで、スパッと授業をやめるのが、担任先生の潔さ。

では、明日、公式にまとめましょう。

 

あと5分あったらなあ・・・と校長が残念に思っていると。

あきらめきれない子どもたち。

どこそこで、子ども達は、議論を続けていました。

 

公開２日前の「わさび」の授業。

クロームブックで「微細な変化」をとらえる授業。

担任が「先を読んで」設計図を立てた授業。

「先生が脇役」

子どもが主役の授業！

・・・ここにあり！

  

金曜日の公開授業、お楽しみに！

 

※　台形の面積の公式

　　（上底＋下底）×高さ÷２

　　だから、上辺という造語がすごいと思うのです。

 

by　校長