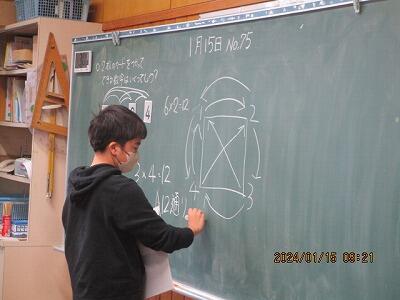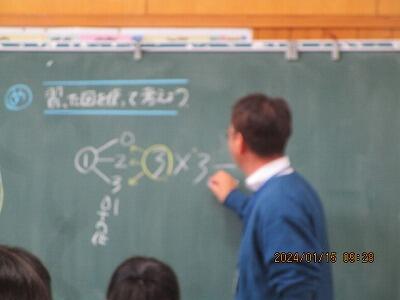2024年1月の記事一覧

６年生の「わさび授業」が、完成の域に近づきました。

仲間との協働学習もすっかり様になり。

主体的なコミュニケーション態度もピーク値に近づいています。

 

さて。

長くなります！

正統。久しぶりの６年生「わさび」授業。

はじまり、はじまり・・・。

 

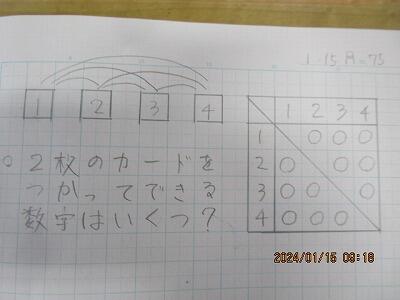
【問題】

１、２、３、４のカードを使って、できる数字はいくつでしょう？

６年生、一生懸命に考えていました。

えっと・・・。

図を使うとこうなるから・・・。

見事な樹形図です。

御指名を受けた子どもさん、発表です。

ということで、こうなります。

答えは・・・。

それぞれに、３個ずつあるから・・・。

担任先生。いつもの定位置。教室の後方に構えます。

次のお子さんには式を発表させます。

だから、３×４で、１２です。

このステップで担任は、必ず聞きます。

「ここまで、分かった人。」「わからない人。」

「解き方・考え方について、友だちに説明してみよう。」

このステップがとても重要な「協働学習」となります。

 

飽きの来ない、自分・全員が主役の活動の開始です。

子ども達、一斉に「組み合わせ」について協議を始めます。

４つ数字があって、それぞれ、３つずつ組み合わせられるから。

３×４で、１２通りだよ。

全員が完全に理解するまで、リフレインが続きます。

まさに、子ども達。

学習を「楽しんで」います。

はい、では、再度、前で説明してください。

十の位の一つの数字に一の位の数が３つあって。３×４で、１２です。

みんな、分かったようですね。

では、違う方法で解いた人の解法を見てみましょう。

担任の「先を読んだ」「子どもの微細な変化をつかまえた」

意図的指名です。

一つの解法で満足しない。

追究を続ける。

この態度が、子どもが主役の授業の原動力です。

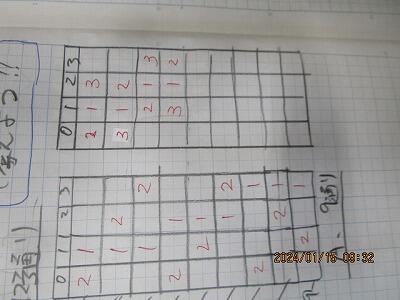
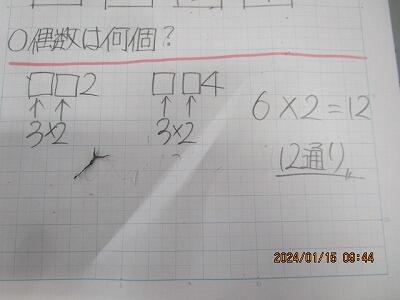
線で結んで考えます。

こうやって結ばれた数字の組み合わせは、６通り。

逆を考えて。

６×２で、１２通りです。

この子どもさんのノートは次のとおり。

確かに、計算式ではない解法です。

担任、この子どもさんの反応を見落とさず、皆に考えさせたかったのです。

担任は、さらに、後一人を指名。

君も、違う考えで解いているね。どうぞ。

指名された子どもさん、うれしそう。

このように、担任は、授業の先を読み、微細な子どもの変化をキャッチする。

これを繰り返すと、必然的に、子どもに自信がつき、子どもが主役になろうとする意欲が芽生え。

「子どもが主役のわさび授業が生まれていく」のです。

 

新しい解法の発表に、教室中が注目です。

誰一人、目をそらす者は、ありません。

ある図が描かれて。

さあ、説明を始めよう、という、その時。

担任の作戦が始まります。

「この図の意味が説明できる人」

はい、そこで、発表男子君の役割は終了。

友だちと説明し合いなさい、という協働学習のステージに、授業は移行します。

この矢印を数えていくと・・・。

こうだから、こうなるよね。

発表者を主役にしない、全員が主役の授業。

そして。やっと、発表男子さんに再度、発表のチャンスがやってきて。

こう数えると、１２通りになります。

・・・。

さて、一通り、解法は出尽くしました。

 

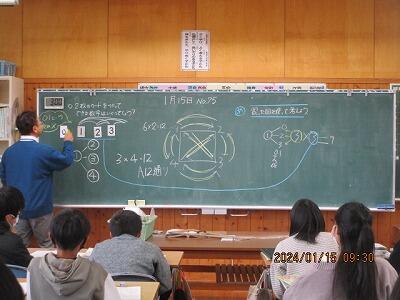
そこで、担任は、次なる課題を示します。

 では、こうなったら、どうなりますか？

一つの数字が「０」になりました。

偶然に、この課題が出されたかのような、自然な問題提示。

ところが。

じつは、この問題こそが、教科書が提示する、今日の本論問題だったのです。

この問題をダイレクトに与えることもできるでしょう。

でも。

このように、子ども達の意欲を徹底して引き出し、レディネスを整えた上で問題を提示すると・・・。

子ども達は、その問題を「解きたくて、説明したくて、ヒーローになりたくて」

つまり。

学習意欲は、クライマックスに高まるのです。

協働学習を通して、子ども達は、意欲的に、主体的に、本論の問題に挑み続けます。

この姿こそが、「子どもが主役の授業」の到達点なのです。

さあ。

説明を始めましょう。

みんなで、楽しく学び合いましょう。

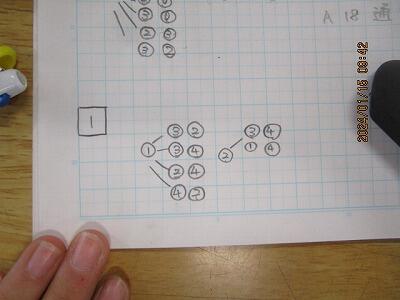
樹形図を使って。説明をします。

解答は、すでに３×３＝９と出ています。

でも、それを、こだわりぬいて、さらに高めようと。

友だちのサポートを借りて、正解にたどり着こうと「あがく」のです。

この「あがき」がとても楽しいのです。

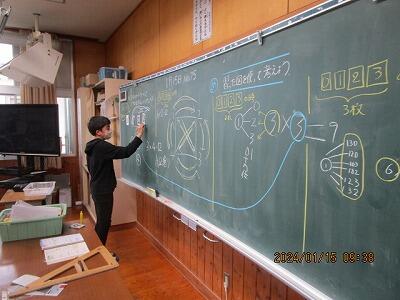
めずらしく先生が、直接的に黒板に近寄りました。

「この３の意味は何ですか？」

さあ。本日のメインイベントです！

子ども達は「３の意味」について、真剣に協働学習を行います。

さあ、子どもさん、指名を受けました。

みんなの視線が集まります。

この３の意味は。

この３つの数字です。

ダイナミックな線で二つの「物」が結ばれました。

なるほど。これは。

これなのか。はあ、すごいね。

実は、先を読みつくしている先生。

次に移ります。

では。

・・・えっと・・・これではどうでしょうか？

２を３に訂正し、「微妙に質的変化した問題」を提示します。

子どもと共に学びながら、ナチュラルに生まれた問題でしょうか？

いえ、いえ、違います。

皆さん。

この下の問題をご覧ください。

この問題は、教科書に提示された、最終問題なのです。

子ども達は、そうとは知らず。

授業の流れから、必然的に発生した、新たな問題に意欲的に挑みます。

「先を読んだ授業」とはこうあるべきなのです。

みな、必死に、最終問題にくらいつきます。

 

誰一人話す者はおらず。

自力解決に身を委ねます。

今日のこれまでの「学習」を「次のステップに生かす」ために。

解法は、今日学んだものを使い、各人様々です。

樹形図の者もいれば。

表組の者もいる。

子どもが主役の授業では。

答えは同じでも。

解法は様々になりがちです。

それが、数学を日常で扱う。

という意味なのです。

算数の学習は、明日の学習の「基礎」となり。

これからの生活の「基礎」となるのです。

さあ。

もう書くスペースがない、この黒板で、ラスト勝負が始まります。

指名を受けた子どもさん、飛んで登壇します。

教師は、再度、「脇役」ポジションに移動します。

こう考えます。すると、一つの先頭の数字に６通りの数字が組み合わせ出来ますよね。

だから。

式は、６×３となり。

１８となります。

担任は、手をゆるめません。

次から次の子どもさんへ、説明を行わせます。

だから。

問題は、この「３」の意味なんです。

「３」は、実は。

ここにつながるのです！

線でつながった。

一つの真理。

この問題。

子どもが主役の授業により。

深く、子ども達の脳裏に焼き付けられました。

 

ここで・・・。５分の残り時間。

担任が動いた。

では。

子ども達、一斉に解決に飛びつきました。

子ども達の回答が早いことに驚きました。

繰り返された今日の学習により、深い学びが生まれているのですね。

みんな、真剣に解いていました。

さあ、そろそろ、時間です。

ラストバッターの登壇です。

偶数ですから。

一の位は２つしかありません。

一の位を２とすると、百の位と十の位は、３×２で６。

担任先生、ここでも、発表者をじらせます。

時間がない。全員、話し合って！

もう、みんな、必死です。

１２の求め方を様々に話し合います。

発表者、最後のまとめです。

担任がサポートに入りました。

だから・・・。

１２なのかな？？？？

 

というところで。チャイム。

この先生。絶対にチャイムで授業を止めます。

 

「では、この続きは、また、今後としましょう。」

 

子ども達にどんな感情が巻き起こるか？

号令後も、この問題について、協議が続くのです。

校長は、何回もこのシーンに出くわして。

分かってきました。

チャイムで、最も盛り上がった子ども達の思考を断ち切る。

すると、次の授業への「猛烈な意欲」が継続する。

 

ひょっとすると。

６年生の算数授業が、「いつもチャイムで中断」するのは。

実は、先生の作戦なのでは・・・？？？

 

なるほど。

教師が「先を読む」と。

このように、ドラマティックな展開が続いていくのですね。

 

６年生が完成に近づいた。

子どもが主役の授業。

 

「わさび」の授業。

「教師は『脇役』に徹する」

「子どもの『微細な変化』に気づく」

「教師は常に『先を読み』授業を構築する」

 

６年担任先生。

見事也！

 

・・・まとめ、つかれまひた・・・。(*_*;

 

by　校長